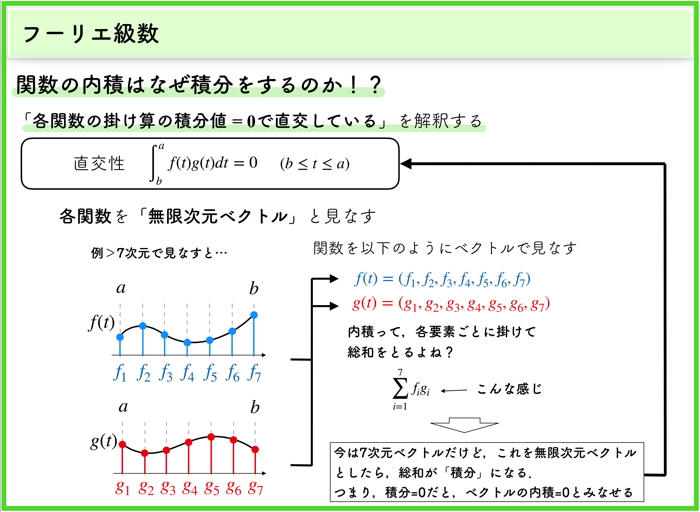
- 非線形最適化問題を扱っている人
- ダウンヒルシンプレックス法の内側の操作について知りたい人
- 数学や物理が好きな人
こんにちは．けんゆー（@kenyu0501_)です．
今日はダウンヒルシンプレックス法という非線形最適化問題によく使用される手法について書きたいと思います．
まずはサクッと非線形最適化問題について説明した後に，ダウンヒルシンプレックス法について詳しく解説していきたいと思います．
非線形最適化問題
非線形最適化問題とは，「目的関数が非線形であり，制約条件がない場合の問題です．
この問題を解く際に，大きく分けて以下の2つの手法があります．
- 勾配法
- 直接法
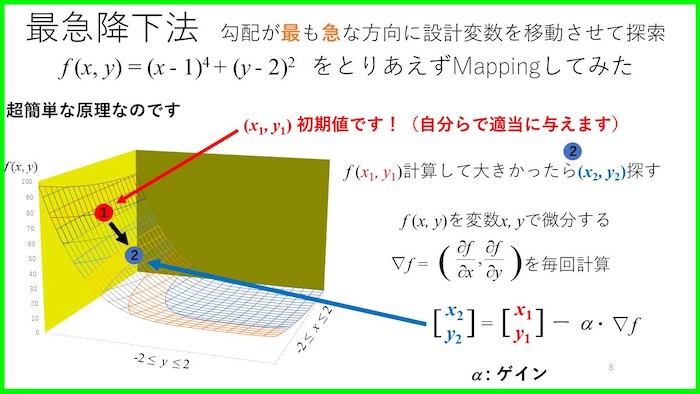
勾配法とは目的関数の導関数を用いて設計変数を探す探索手法です．
今回は，勾配法は説明しませんが，例えば，最急降下法などが有名どころです．
この記事はこんな人にオススメです． 「最急降下法」を理解したい人 「最適化」に関しての定義を理解したい人 数学…
(知りたい人がおられましたら，こちらをご覧ください)
直接法とは，目的関数の値だけを頼りに探索する方法です．
目的関数の微分などを行いません．
ただ単に，目的関数の値を小さくするような設計変数の探索を行います．
直接法で関数を作る例
直接法で関数を作る，そして関数の中の設計変数を適切に決めるためのちょっとした具体例を書いておきます．
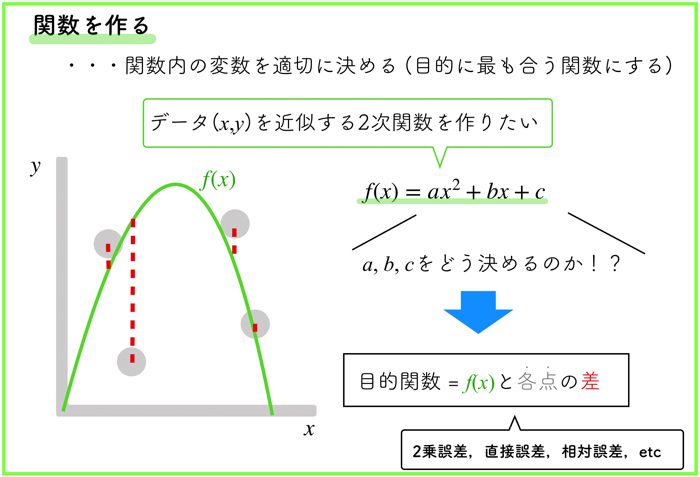
以上のように，\(x\)と\(y\)を変数にもつデータ群を上手く近似するような2次曲線を考えます．
その時に，内側の設計変数(パラメータ)\(a,b,c\)をどのように決めるのかが問題になります．
だいたいは，最小二乗法などを使って，Excelなんかで計算すると早いのですが，もっと複雑な式になるとそうはいかない場合も多いです．
ということで，目的関数を導入して，その目的関数を小さくするような他の最適化手法で，\(a,b,c\)を決定することは価値があったりします．
目的関数の取り方自体は，絶対誤差でも良いですが，だいたいは誤差の2乗をする場合が多いですね．
実験データと近似関数\(f(x)\)の誤差の取り方によっては，プライマイナスが出て，誤差が相殺される場合があるからです．
ダウンヒルシンプレックスの特徴
では，早速，ダウンヒルシンプレックスについてやっていきましょう．
ダウンヒルシンプレックス法は，「滑降シンプレックス法」や「ポリトープ法」，「ネルダーミード法」などと言われたりもしますが，全て同じです．
ただし，線形計画法の一つであるシンプレックス法とは全く違うで，注意が必要です．
ダウンヒルシンプレックス法の全体像の説明
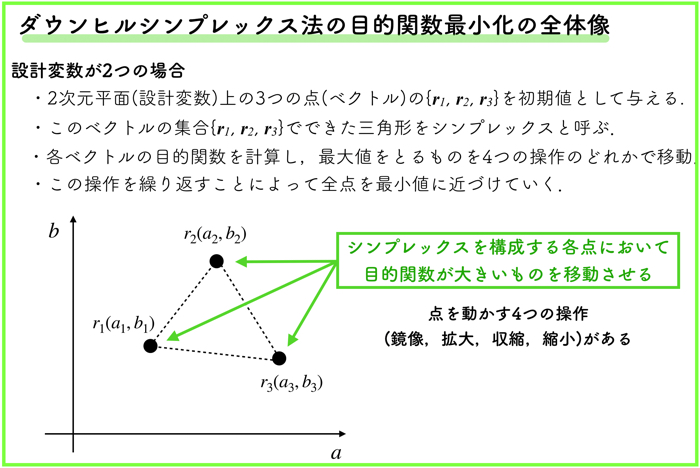
ダウンヒルシンプレックス法の目的関数最小化の全体像です．
わかりやすいように，設計変数が2の場合で全体像を説明していきます．
- 2次元平面(設計変数)上の3つの点(ベクトル)の{\(r_1, r_2, r_3\)}を初期値として与える．
- このベクトルの集合{\(r_1, r_2, r_3\)}でできた三角形をシンプレックスを呼ぶ．
- 各ベクトルの目的関数を計算し，最大値をとるものを4つの操作のどれかに移動．
- この操作を繰り返すことによって全点を最小値に近づけていく．
ちなみに，設計変数が2つの場合は，初期値のベクトル(2つのスカラー変数をもつ)は3つ必要です．
この初期値に必要になるベクトルは(設計変数の数+1)の数が必要になります．
これは，シンプレックスを動かす際に，(設計変数の数+1)だと，シンプレックスを動かす操作がやりやすいからです．
設計変数の数と同じ数の初期値のベクトルだと，移動するベクトルをどのように動かして良いか迷います．
ダウンヒルシンプレックス法の4つの操作に関して
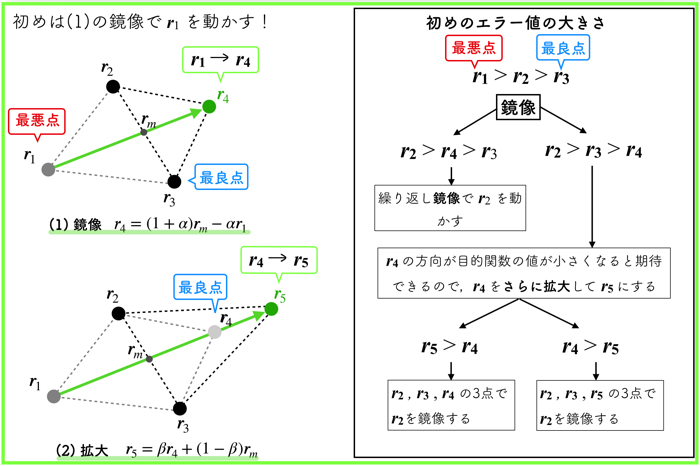
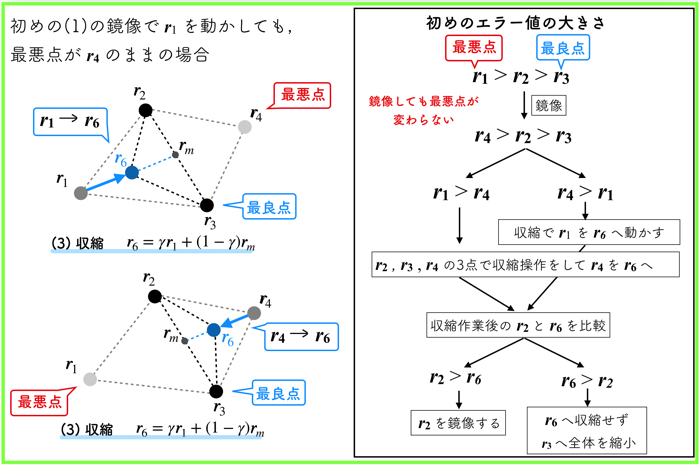
いかにダウンヒルシンプレックス法の4つの操作(鏡像，拡大，収縮，縮小)についてまとめておきます．
この4つの操作で，パラメータの探索を行います．
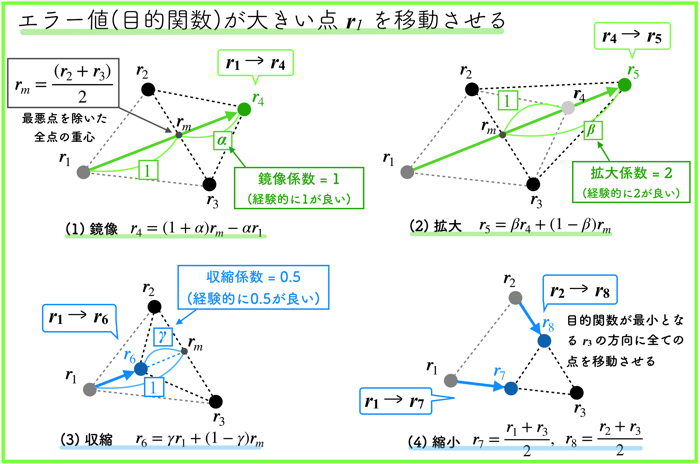
\(r_1, r_2, r_3\)のベクトルを初期値として与えていますが，\(r_1\)がもっとも目的関数が大きいベクトルになります．
目的関数が大きいということは，誤差が一番大きいベクトルということなので，\(f(x)\)のパラメータとしては適切ではないということになります．なので，r1を動かして，エラー値を下げるということをします．
基本的には，一番初めは，鏡像という操作をはじめにこないます．
以下の3つのスライドに，4つの操作の具体的順番を記述するので，ご覧ください．
