2次元非線形の相平面をPythonで書く

この記事はこんな人にオススメです

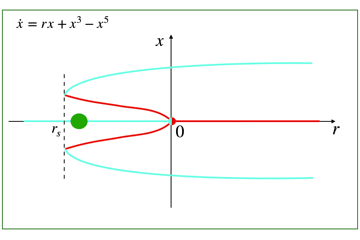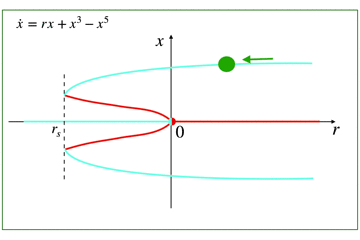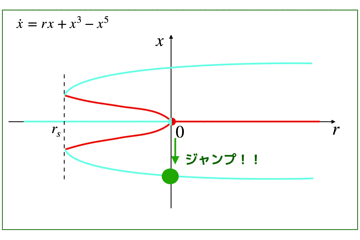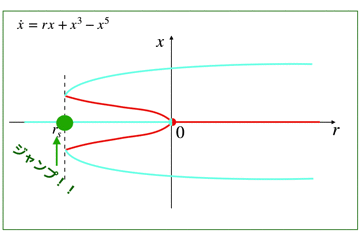
工学とか数学とか物理とかが好きな人
線形系とか非線形系について興味がある人
相平面についてちょっと知りたい人

こんにちは．
以前は２次元線形系のお話をいくつかしました．
（参考：線形系のもう少し進んだ分類）
（参考：２次元線形系ダイナミクスの安定性の図的理解と専門用語について）

そこで本日は非線形系の相平面について少し取り上げます．
（参考図書：「ストロガッツ非線形ダイナミクスとカオス」）

相平面におけるベクトル場に関しては，以前の線形系の記事をいくつか一度読んでおけばすんなり理解できると思います．

相図の復習

相平面におけるベクトル場の一般的な形はこのようにかけました．
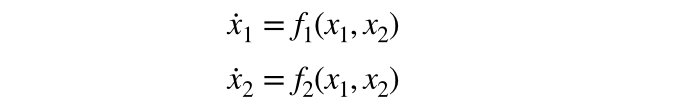xは，相平面上の点を表し，その一階微分(xのdot)はその点における速度ベクトルを示します．

各点xをベクトル場に沿って流すと，相平面の中をグニャグニャと曲がりくねったり，直線的に進んだりする解の軌道が得られるはずです．
これは，定性的な解の見方ですが，非線形系は解析的に解が得られない場合がほとんどなので，相図はかなり役に立つ情報です．

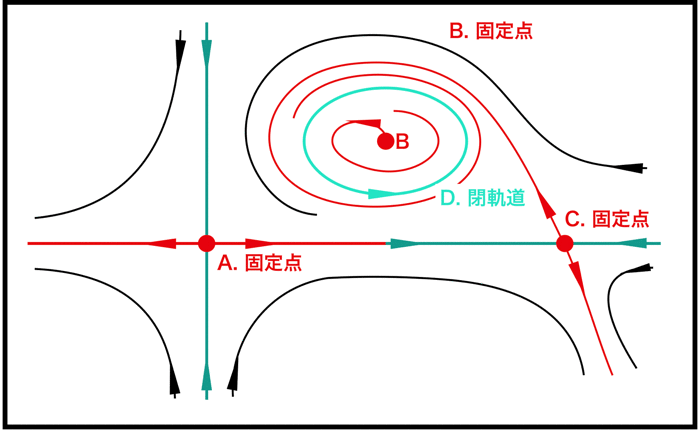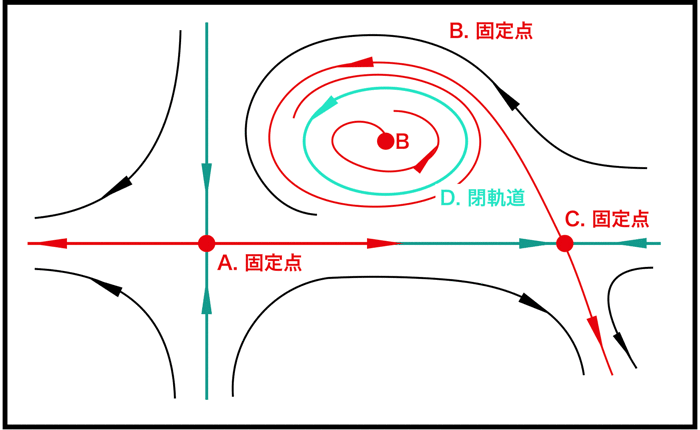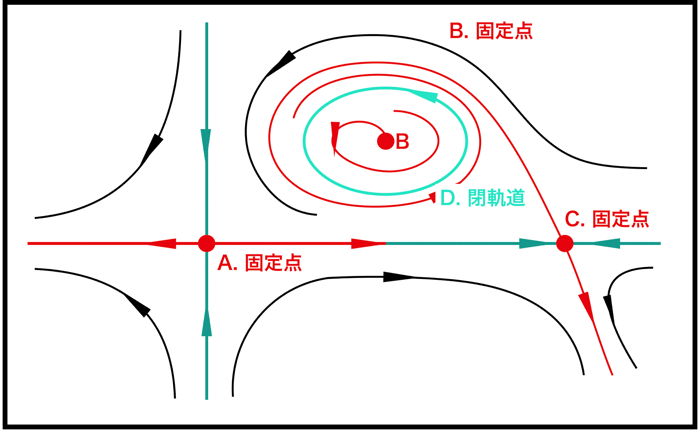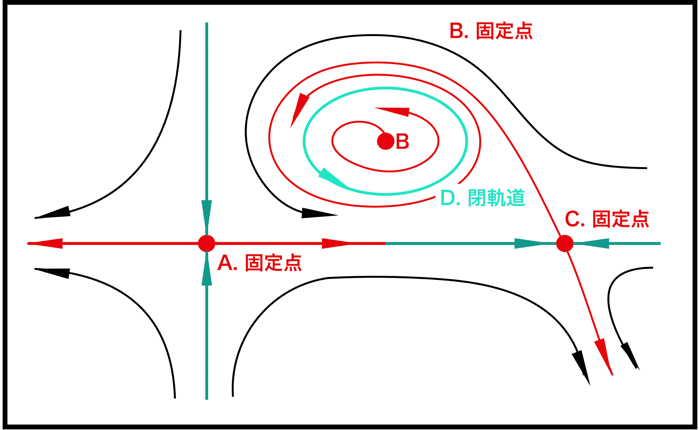
また相図に関しては多くの種類がありますが，代表的なものを以下（A~D）に示しておきます．
（以下の図は，相図の固定点を例題的にいくつか示すものなので，同時にそれが存在するものではありません）

A，B，Cは系の固定点（定常状態や釣り合いの状態）です．
しかし不安定固定点です．
近傍の流れが固定点から遠ざかろうとしているためです．
AとCの固定点の近傍の流れはほとんど似てますが，Bの固定点の近傍の流れは違います．

Dは閉軌道であり安定です．
周期解を示します．

上に示したA~Dの他にも，相図にはいろんなパターンがありますが，だいたいこのようなものです．

数値計算をして相図を見る

ここでは本書「ストロガッツ非線形ダイナミクスとカオス」で紹介されている以下の問題を数値計算によって計算してみます．

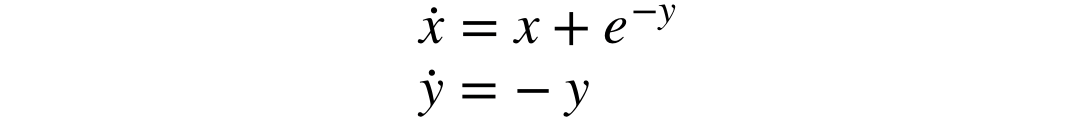
以上の式を連立して，各速度ベクトル＝0を解くと，解は(-1,0)になります．
相図の様子を以下の図に示します．
ちょうど，x＝-1，y=0で不安定な固定点であることがわかります．
また，方向場を同時にプロットしてます．
（プログラムは最後にあります）

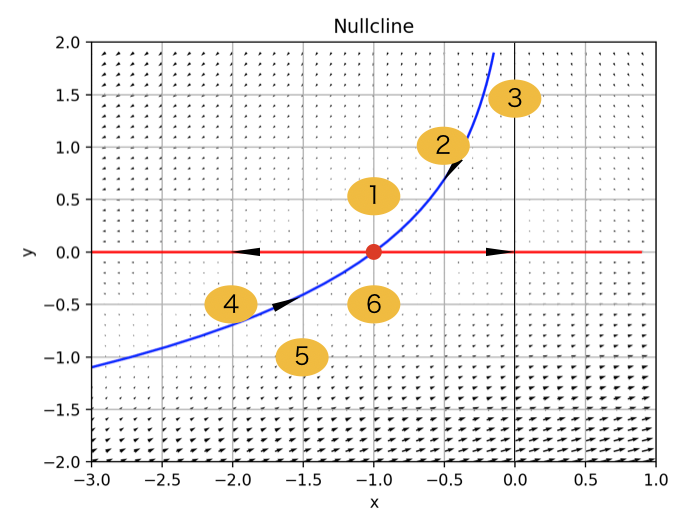
また，上の図の濃い青，濃い赤で示したラインはヌルクラインとって，相図をより一層見やすくするものです．

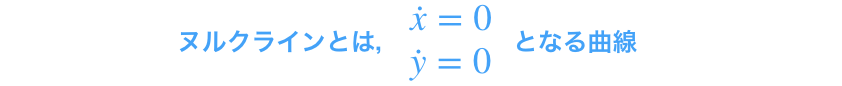
xおよびyそれぞれの微分値（速度）が0になるラインを決めてます．

さて，ここで，上に示した図のオレンジの番号１〜６の初期条件（x0, y0）を与えて，数値解法により解の様子を確認していきましょう．
結果を以下に示します．

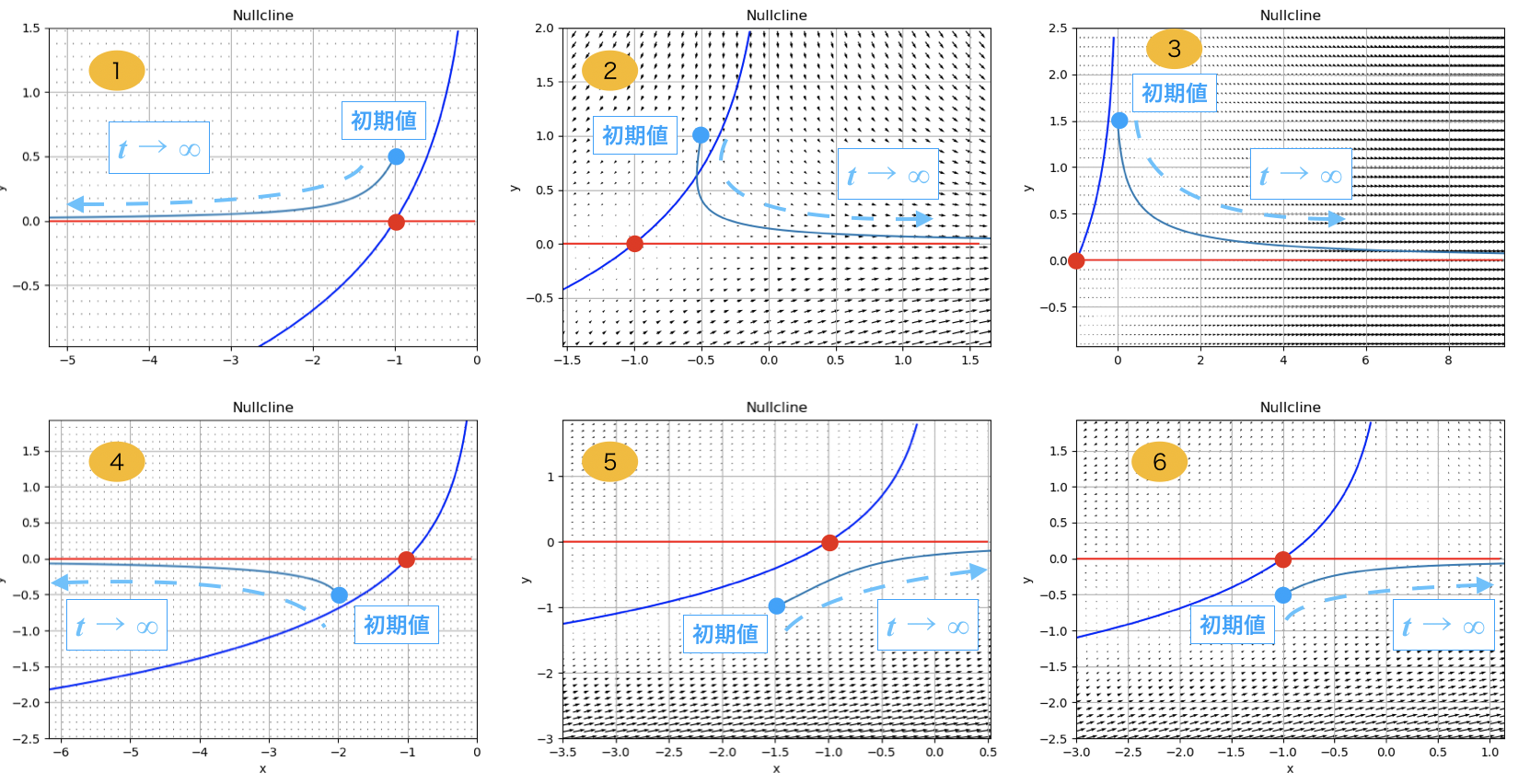
薄い青色で示したのが，解の軌跡になります．
t→∞で，ベクトル場の中をどのように進んでいくのかがわかります．
(-1,0)は不安定固定点なので，各初期値から始めた軌道はt→∞で離れていく様子が確認されます．

つまりこの系は，青いヌルクライン以外の箇所で初期値を与えると，系は固定点から離れていくというのが，数値計算で確認できます．

プログラムに関して

Pythonですが，プログラムを貼っておきます．
興味がある人は，いろんな初期値やいろんな非線形系の式を試してみてもいいかも知れません．
初期値は，不安定固定点に設定してあるので，色々と動かしてみると良いかもです．

import numpy as np
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
import scipy.integrate as integrate


def dx(x, y):
    return x + np.exp(-y)

def dy(y):
    return -y

def vector(state, t):
    x, y = state
    nextx = dx(x,y)
    nexty = dy(y)
    return nextx, nexty

#初期値は不安定固定点
x0 = -1.0
y0 = 0.0

t = np.arange(0.0, 2.0, 0.01)

v = integrate.odeint(vector, [x0, y0], t)

x_vec = v[:,0] 
y_vec = v[:,1]

plt.figure()
plt.plot(x_vec, y_vec)
plt.xlabel("x")
plt.ylabel("y")
plt.title("Nullcline")

#作図範囲を設定するパラメータ
p = 2.0
xmax, xmin = x_vec.max() + p,  x_vec.min()- p
ymax, ymin = y_vec.max() + p,  y_vec.min() - p

X, Y = np.meshgrid(np.arange(xmin, ymax, 0.1), np.arange(xmin, ymax, 0.1))
dX = dx(X, Y)
dY = dy(Y)
plt.quiver(X, Y, dX, dY)

plt.contour(X, Y, dY, levels=[0], colors="red")
plt.contour(X, Y, dX, levels=[0], colors="Blue")
plt.xlim([xmin, xmax])
plt.ylim([ymin, ymax])
plt.grid()
plt.savefig('test.png')
plt.show()