2重井戸を左右に揺らしてみるよ（Duffing型の非線形振動子で確認）

この記事はこんな人にオススメです

井戸型ポテンシャルに興味がある人
モデルやシミュレーションが好きな人
非線形系が好きな人

こんにちは．けんゆーです（@kenyu0501_)
前回やった2重の井戸型ポテンシャルのアナロジーを確認していきます．
（参考：2重井戸ポテンシャルV(x)の相図でホモクリニック軌道を見る）

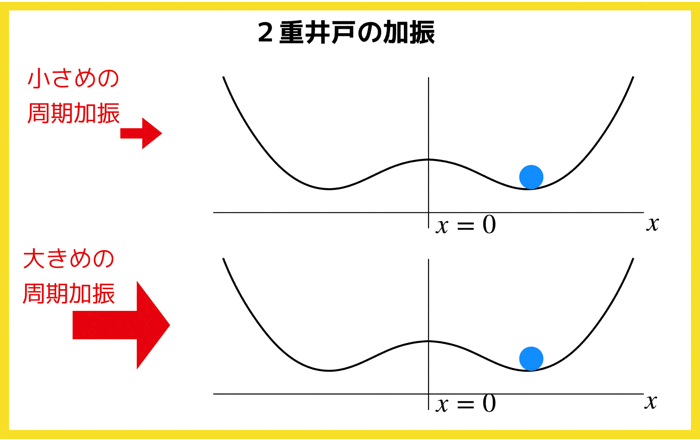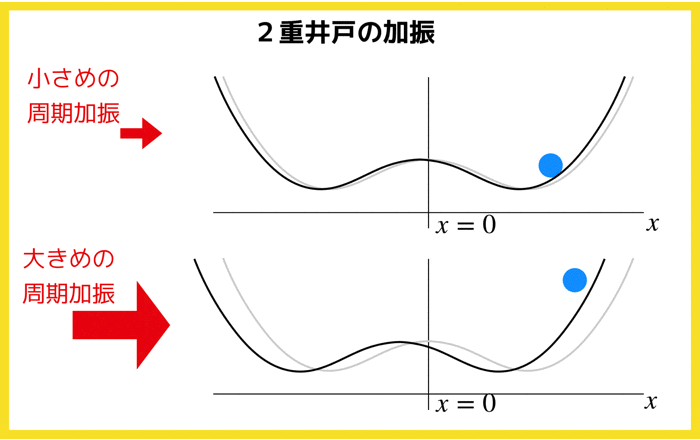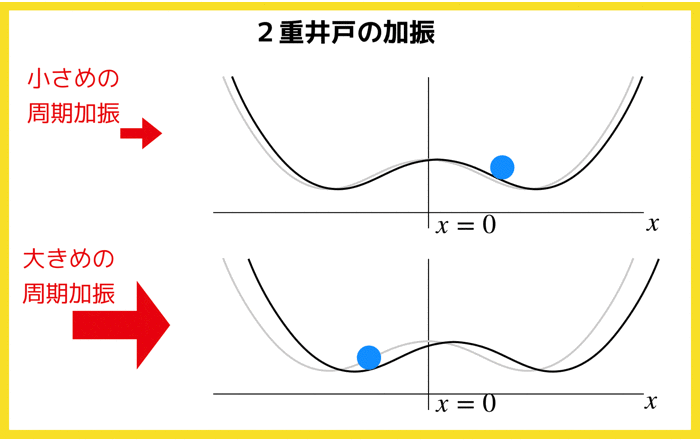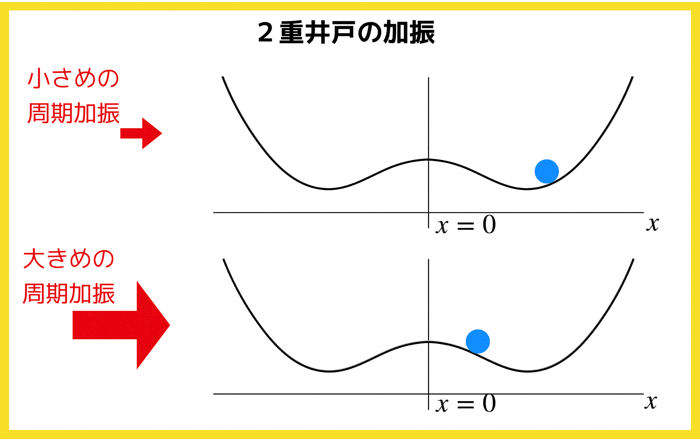
２重井戸は以下のようなものでしたね！

本日はこの２重井戸を左右に周期的に揺さぶったとき，中にある粒子はどのような挙動を示すのかを考えていきます．

図的理解

やりたいことを簡単に整理するとこんな感じです．

２重の井戸型ポテンシャルに小さめの加振と大きめの加振を与えると粒子の挙動xはどのようなものになるのか？
ということを確認したいです．

ではでは，物理的な予測を立てます．

加振が弱いと粒子は片井戸の底で少し揺れるだけ（リミットサイクル的）
加振が強いと粒子は一方の井戸を飛び越えて反対側の井戸へ行く．

他にも関心としては

もし粒子がコブの頂点に登るギリギリ足りる程度のエネルギしか持たない場合はどうなるのか？
この系の外力と摩擦が上手くバランスしていれば，外力の微妙なタイミングによって，粒子は片方へたまたま落ちたり，
また，たまたま，こぶを登りさらにもう片方へ落ちる．

みたいな状況が繰り広げられそうです．
（参考：「ストロガッツ非線形ダイナミクスとカオス」）

さてさて，モデルを組んでみましょう．

モデル

２重井戸のポテンシャルは以前の記事でやりましたね！
（参考：2重井戸ポテンシャルV(x)の相図でホモクリニック軌道を見る）

この２重井戸ポテンシャル中の粒子の従うニュートン法則ということを見なして，以下の方程式を導出します．

これは，1979年にMoonとHolmes氏がモデル化したようです．
原著論文はこちらです．
（「A magnetoelastic strange attractor ，F. C. Moon, P.J.Helmes, 1979. 」）

まぁ，この式をパッと見て
あっ！！Duffing振動子だ！！！
となる人はその道の人だと思ってもらっても良いと思います．

ここで，モデルパラメータについてまとめておきます．

A>0・・・摩擦による減衰係数
F・・・外力の強さ
ω・・・外力の振動数

数値シミュレーションでは，A=0.25，ω=1に固定して，外力の強さFを色々と変化させます．
（参考：「ストロガッツ非線形ダイナミクスとカオス」）

粒子の変位xは動く座標系に相対的なものです．

シミュレーション

F=0.18（弱い加振）

まず初めに「ストロガッツ非線形ダイナミクスとカオス」の例題12.5.1 に見習って，F=0.18で加振します．

粒子の初期条件(x, v)=(0.0)です．
周期加振によって粒子は振る舞います．
xは位置，vは速度(xの一階時間微分)を表します．

では，結果を見ていきましょう．

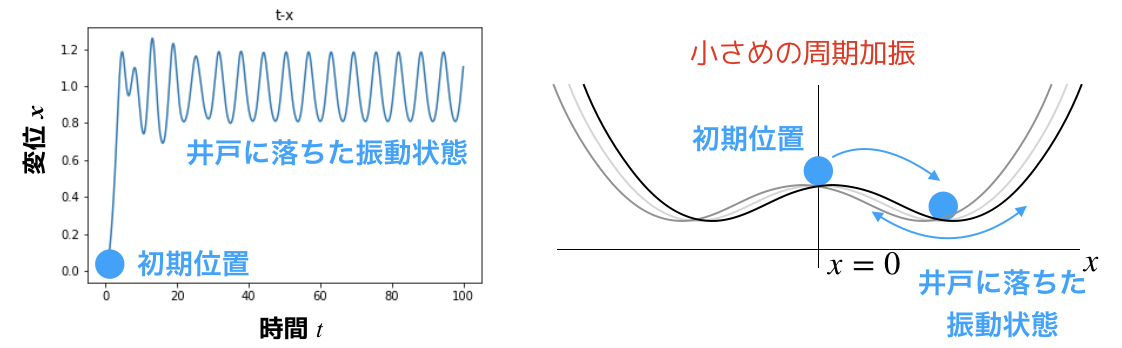
予想通りといえば予想通りです．
t→∞にした時の解は，ある周期解に収束しますね．

ちなみに，変位-速度の相図を見てみましょう．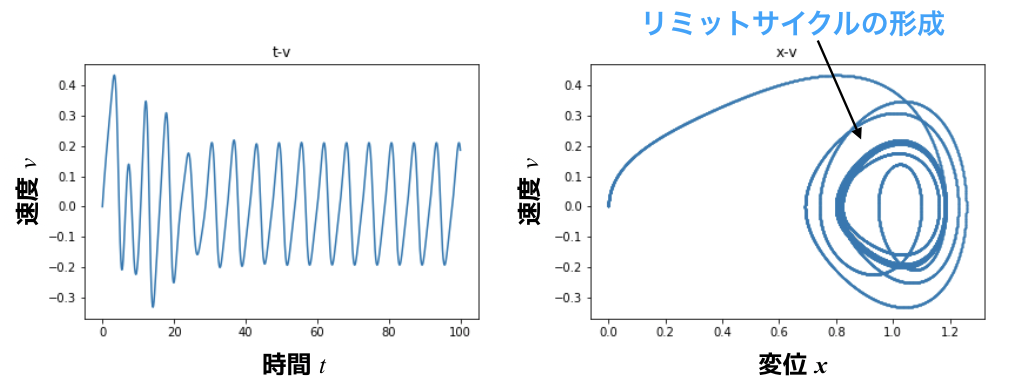

t→∞にした時の解は，ある周期解に収束するので，位相平面上はリミットサイクルを形成します．
リミットサイクルを知りたい人はこちら
（参考：「リミットサイクルは自励振動をする凄いやつ」）

つまり，何が言いたいかというと，この系の解は，加振力が弱い場合，安定した周期解になるということがわかります．
このリミットサイクルは安定です．
（リミットサイクルに向けて軌道が向かっているので）

リミットサイクルは本質的には非線形現象で，線形系ではみることができません．
では，もう少し加振力を大きくしてみましょう．

F=0.40（強い加振）

先ほどの倍以上の周期加振をこの系に加えます．
粒子の初期条件(x, v)=(0.0)です．

では，結果を見ていきましょう．

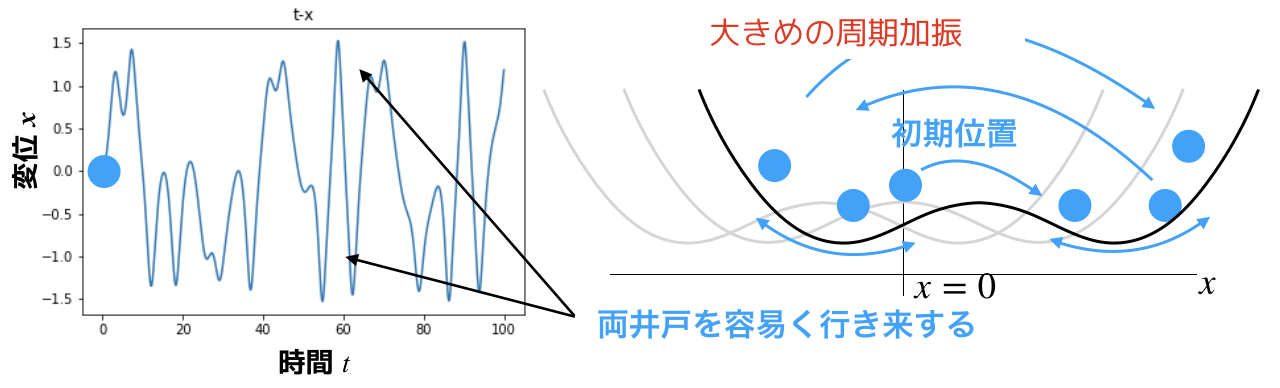
こちらも予想通りの振る舞いです．
周期的とも，何とも言えぬ軌跡です．
加振力を大きくしていけば，井戸と井戸の間にあるコブを飛び越してしまうので，xの軌道はプラスに行ったりマイナスに行ったり，カオス的な振る舞いになります．
これは，Duffing振動子の振る舞いの理解の手助けになるのではないでしょうか．

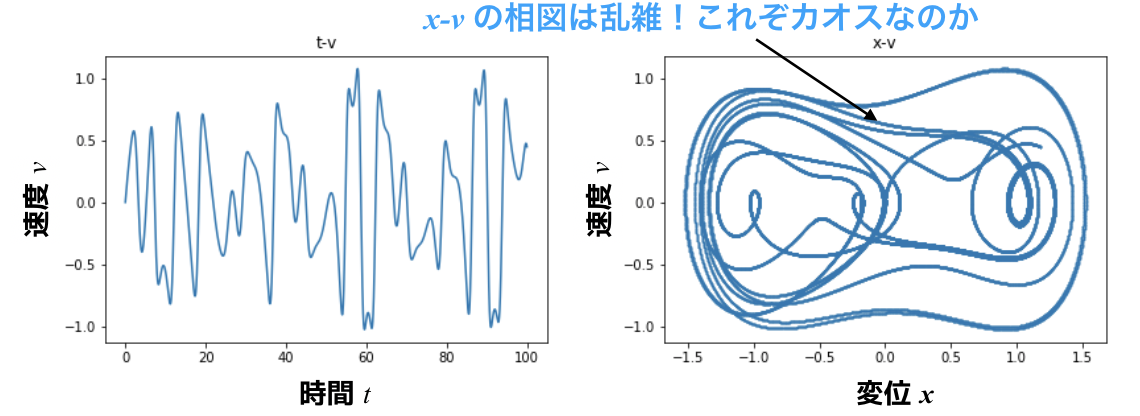
相図に関しても，かなり複雑です．
加振力が小さい時には，リミットサイクルを形成していましたが，ここではなんとも言えない美しい形状（おいらだけ？笑）を書きます．

果たして，これは安定なのか？？？？

全く安定とは言えませんね．

解がわかりません．
この状態，初期に大きく依存して形状が変わってきます．
周期加振が小さい時には，ある程度違った初期値をいれても，リミットサイクルを形成すると考えられるので解は周期解で安定しますが，この場合は完全にわかりません．

では，この状態は解析ができないカオスとして片付けてしまうのか？
まあ，それでも良いですが，この相図に時間的な概念をもう一度埋め込んで，非自律系（周期外力があるので）の相図を見る工夫だけでもしましょう．

ポアンカレ断層を使う

周期的な加振が加わった非自律系の相図の見方は，ポアンカレ断層と呼ばれる味方をすると何かしら見える可能性があります．
ポアンカレ断層は，tが2πの整数倍となる時の(x,v)を書き出す単純な方法です．
つなり，外力で駆動されるサイクルの同じ位相時間ごとに，相図を書き出すのです．
これ⬇︎

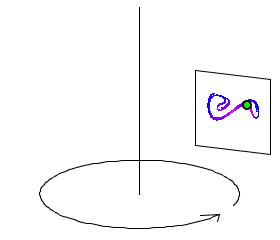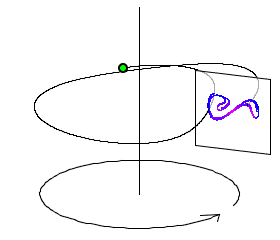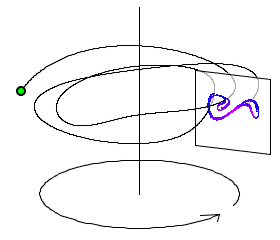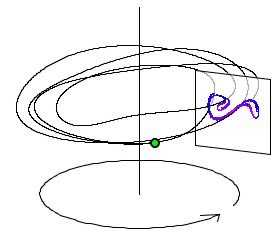画像はScholarpediaから抜粋しました
（参考「Duffing oscillator」）

ちょっと見てみましょう．

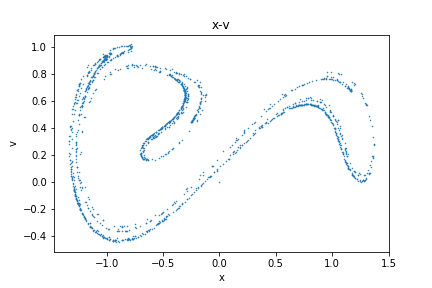
こうなりました．
さっきみたいに絡み合ってはないですね．
しかし，これが安定なのか不安定なのかを問われるといまだにちょっと疑問ですが，カオスである系ということを断定することができます．
こういう形状のものをストレンジアトラクタと言います．

どういうことかというと，
これは，一番初めに示したモデル式のストレンジアトラクタの断面と解釈します．
周期外力を小さい状態から大きく状態へ変化させると，相図はリミットサイクルからストレンジアトラクタになるのです．

F=0.255（中くらいの加振）

中くらいの，って言葉がなんか幼いですが許してください．
リミットサイクルと，カオス的な挙動であるストレンジアトラクタの中間地点を少し解析してみましょう．
初期条件はこれまでと同じです．

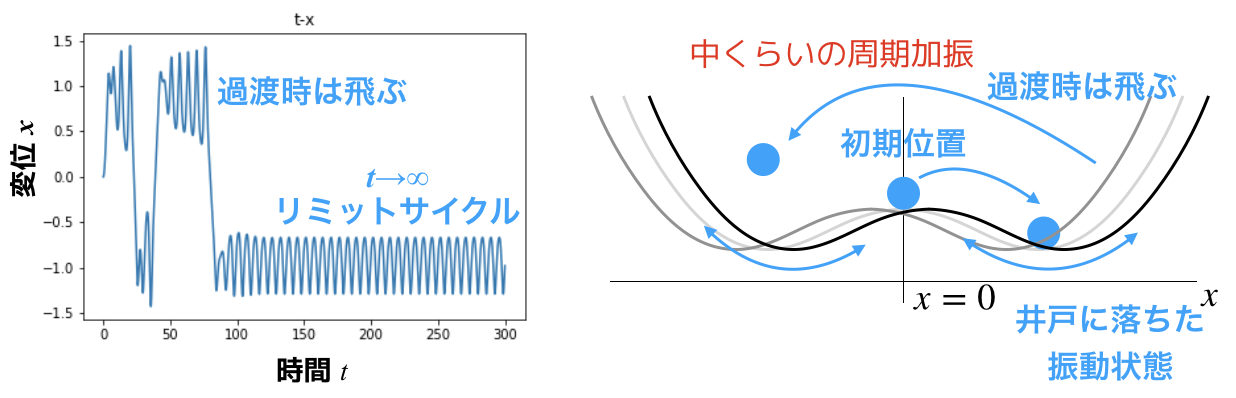
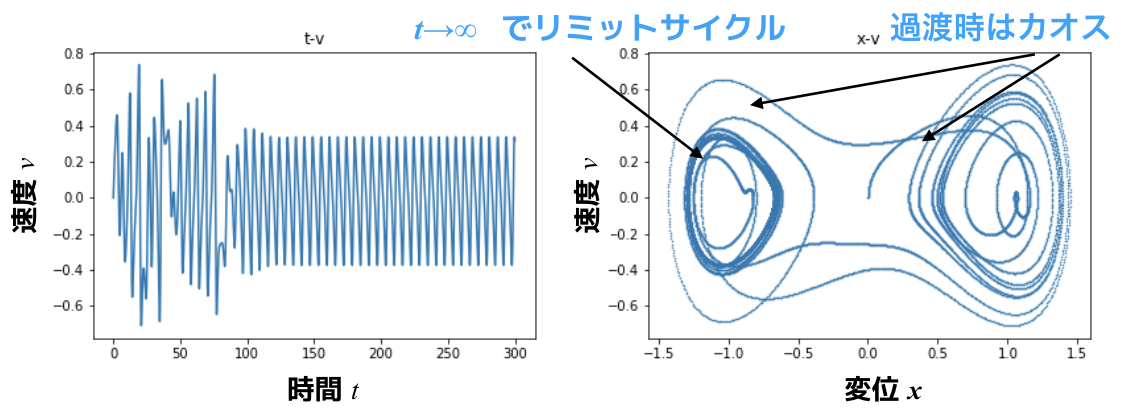
こういう感じになります．
初めの状態（過渡時）ではコブを超えていきカオス的ですが，時間が経つとリミットサイクルを形成します．

面白いですね．

こういうのを過渡カオスっていいます．
この過渡カオスが起こる系でも，最終的に選ばれる系の状態は初期値に大きく依存します．

プログラム載せておくので，時間があればやってみてくださいね！

Pythonプログラムについて

こちらです〜

from scipy.integrate import odeint
import matplotlib
matplotlib.use('Agg')
import numpy as np
import matplotlib.pyplot as plt

A = 1/4
B = 1.0
C = 1.0
P1 = 0.18
omega = 1.0
fai = 0.0

dt = np.pi/250
var = [0.0,0.0]

t = np.arange(0, 100, dt)

def duffing(var, t, A, B, C, F0, omega, phi):

    dx = var[1]
    dv = -A*var[1] +B*var[0] - C*var[0]**3 + P1*np.cos(omega * t + phi)
    
    return np.array([dx, dv])

var = odeint(duffing, var, t, args=(A, B, C, P1, omega, phi))

x = var[:,0] 
v = var[:,1]

plt.figure()
plt.plot(t, x)
plt.xlabel("t")
plt.ylabel("x")
plt.title("t-x")
plt.savefig('t-x_f=018.png')
plt.show()
plt.close()

plt.figure()
plt.plot(t, v)
plt.xlabel("t")
plt.ylabel("v")
plt.title("t-v")
plt.savefig('t-v_f=018.png')
plt.show()
plt.close()

plt.figure()
plt.plot(x, v, ".", markersize=1)
plt.xlabel("x")
plt.ylabel("v")
plt.title("x-v")
plt.savefig('x-v_f=018.png')
plt.show()
plt.close()